计算机组成小记

Posted on 繁/简： set

困啊，困，困到眼皮咀嚼眼珠，下巴亲吻桌面，意识在困倦中被熬成一锅浓粥，试图清醒过来却拔出粘稠的丝。老师破碎的英语断断续续的传来，像深山中精怪的呼唤；屏幕上的 PPT 变幻扭曲出炫光的轮廓，透过公式和图像我恍惚看到了神谕。

COMP2120 Computer Organization 笔记。无聊的课程前轰然倒塌的我。


  This article is a self-administered course note.

  It will NOT cover any exam or assignment related content.


Digital Logic

Boolean Algebra. 该部分与 COMP2121 之前的命题逻辑部分高度重合。值得注意的是逻辑与 \(\land\) 常被表示为 \(\times\)，逻辑或 \(\lor\) 被表示为 \(+\)，否定 (NOT) \(\lnot A\) 被表示为取补 (complement) \(\overline{A}\)。

Functionally complete sets. (三元) AND, OR, NOT. (二元) AND, NOT/OR, NOT. (一元) NAND/NOR.

Implementation of Boolean function. 将真值表转化为布尔表达式。常用 sum of products (SOP) 方法：

  • minterm: 一个包含所有变量的累乘 (AND) 项。
  • 对所有函数值 \(F=1\) 的 minterm，为 0 的变量取反，为 1 的变量不变，再求和得到布尔表达式。

S-R Latch. 有点像 flip flops，作为记忆单元。

Karnaugh Map. 卡诺图，用于化简复杂的布尔表达式。

  • 二元 \(2^1\times 2^1\)，三元 \(2^1\times 2^2\)，四元 \(2^2\times 2^2\)。
  • 为保证变量的连续变化，表头采用格雷码 (Gray code) 排列。
  • 选出 (数量尽量少的) 若干个全 1 矩形。矩形大小必须是 \(2^n\)，可以相互重叠或者 wrap around 图的边界。
  • 每个矩形对应一个 minterm，忽略 0 和 1 均取到的变量，其他的变量按照之前的规则取反/保留。


Number Representation

radix-\(10\) to radix-\(r\). 对于十进制数 \(A.B\)，分别处理其 integer part 与 fractional part。

  • \(A\): 经典的 quotient remainder 方法。短除后得到的余数记得倒着写。
  • \(0.B\): 不断乘 \(r\)，取整数部分直到 \(B=0\)。

binary to hexadecimal. 从左到右，四个一组，二进制中的每四个数码对应十六进制中的一个数码。记住 \(A-F\) 对应 \(10-15\)。

binary to octal. 从左到右，三个一组。

Excess \(K\) (aka Offset Binary, Biased Representation). 加 \(K\)​ 后再求 bit pattern 表示。

Sign-Magnitude Representation. 难以计算，\(0\) 有两种表示。

One's Complement.

  • 正数：同 unsigned bit pattern。
  • 负数：将 unsigned bit pattern 取反。本质上 \(-x\) 被 \(2^n-1-x\)​ 表示。
  • 仍然存在 \(+0\) 与 \(-0\) 表示，加法实现还是不够直接。

Two's Complement.

  • 正数：同 unsigned bit pattern。
  • 负数：将 unsigned bit pattern 取反后加一。本质上 \(-x\) 被 \(2^n-x\)​ 表示。
  • \(0\) 的表示唯一。由于 \(10...0_n\) 的意义空缺，将其分配给 \(-2^{n-1}\)。因此 2's Complement 的表示范围比之前的两种方法多 \(1\)：\([-2^{n-1}, 2^{n-1}-1]\)。加法计算简洁。
  • Range Extension：使用 sign bit 进行填充。

Floating-Point Representation (Chapter 4.2). 与定点数表示 (Fixed-Point Representation) 相对。定点数表示规定了小数点前后 (整数部分与小数部分) 占据的位数，因此无法较精确的表示 large numbers 或 small fractions。浮点数表示则没有这样的限制。

浮点数表示本质上是二进制下的科学记数法。以 32 位为例，一个浮点数表示分为三部分：

  • Sign of Significand (1 bit) \(S\)：符号位。
  • Biased Exponent (8 bits) \(E\)：幂数位，通常采用 excess-127 表示。
  • Significand (23 bits) \(M\)：又称 mantissa，有效数字位。类似科学记数法，有效数字被 normalize 为 \(1.\text{xx...x}\)。由于 \(1\)​​ 总是出现在首位，它将会被省略。

浮点数表示的实值 (actual value) 计算。

  • 一般来说，实值的计算符合公式 \((-1)^S\times 1.M \times 2^{E-127}\)。
  • IEEE 标准下的特殊值 (special values)：exponent 为全 \(0\) 或全 \(1\)。
    • subnormal values：被 exponent 全 \(0\) 标记，公式变为 \((-1)^S\times 0.M\times 2^{-126}\)。
    • infinity and Not-a-Number (NaN)：被 exponent 全 \(1\) 标记。若 \(M\) 为全 \(0\)，表示 \((-1)^S \infty\)；若 \(M\) 非全 \(0\)，表示 Not-a-Number。
  • 由此可见，有效的 exponent range 在 \([1,254]\) 间。这代表 normal values 的幂数范围在 \([-126,127]\)​ 间。

浮点数表示中精确度 (precision) 与表示范围 (range) 的 tradeoff。精确度与 significand 的位数正相关，范围与 exponent 的位数正相关。


Number Arithmetic

虽然很佩服研究出这些繁琐规则的人，但对这一部分是真的感不起兴趣。

[具体参见 Tutorial-2 slides 与 Chapter 4.3-Number Representation and Arithmetic Part III]

Addition/Subtraction. (1-4 tutorial, 5 lecture)

  • Excess-\(b\)​ Representation.
  • 2's Complement Addition/Subtraction. add bit patterns directly and ignore the carry out.
  • 1's Complement Addition/Subtraction. \(\text{a+b carry out ? (ignore carryout) add 1 back : do nothing}\)​.
  • 2's Complement Range Extension. Fill with copies of the sign bit.
  • Floating-point Addition/Subtraction.
    • align the significands to make two exponents equal (larger one)
    • add/sub on the significand and determine the sign of result
    • normalize (truncate) and rounding

Multiplication/Division. (lecture)

  • 2's Complement Multiplication. 规则很复杂，总的来说是被乘数进行 sign extension，按照乘数的符号位分类讨论，列出竖式进行计算。[见 Chapter 4.3 p.3 multiplication in 2's complement]
  • Floating-point Multiplication/Division.
    • Exponent 部分回到 Excess-\(b\) 表示的加减法。
    • Significand 部分相乘/相除并确定符号。
    • normalize 然后 rounding。


Instruction Execution Cycle

详见 From NAND to Tetris 课程笔记，内容基本重合。

与 Hack computer 的不同之处见 assignment 中提供的 sim.py 和作业描述中的示意图。CPU 中有：

  • PC (program counter)。在 byte addressing 模式下每轮隐式的 \(+4\)。
  • Register File。由少量快速寄存器组成，储存 CPU 经常访问的数据。RFIN 写入，RFOUT1 与 RFOUT2 输出。
  • MAR (memory address register)，存储地址。
  • MBR (memory buffer register)，存储从 memory 中提取的数据。常用 MBR <- Mem[MAR] (operand fetch)。
  • IR (instruction register)，存储 PC 指向的具体指令内容。常用 IR <- Mem[PC//4] (instruction fetch)。
  • 以上的寄存器被若干 data bus 连接起来。

关于指令也有少许不同之处；细节还是参考 sim.py。

  • 1-word instruction. ADD, SUB, OR, AND 等指令均在 1 word (4 bytes) 中指定了两个源地址与一个目标地址。
  • 2-words instruction. LD (load), ST (store) 均是 2-words 指令。第一个 word 指定了 operation code，CPU 地址 (寄存器地址，在 LD 中为目标，在 ST 中为源) 与 addressing mode (总是 0xFF)。第二个 word 指定了需交互的 memory 的地址。
  • 2-word instruction. BR (unconditional), BZ (zero flag is true), BNZ (zero flag is not true) 这些 branch 指令也是 2-words 指令。 第一个 word 指定了 operation code，condition code 与 addressing mode (总是 0xFF)。第二个 word 指定了 jump 的目标地址。


Memory Hierarchy

memory 一直是性能瓶颈的主要来源。memory hierarchy 在成本与性能间找到了一个平衡点。从金字塔的顶端到底端，memory 的成本越来越低，容量越来越大；同时所需的 access time 增加，被 CPU (直接) 访问的频率越来越低。

  • registers of the CPU.
  • on-chip cache memory [inside CPU chip].
  • cache memory [on the motherboard].
  • main memory [on the motherboard].
  • external memory [secondary memory].

对需要频繁访问的数据，例如 temporal locality 与 spatial locality；将它们从 lower level 复制到 higher level 中。

关于 memory byte ordering - 对于 multi-byte data 有两种存储顺序：Big Endian Mode 与 Little Endian Mode。

关于 memory 的种类。

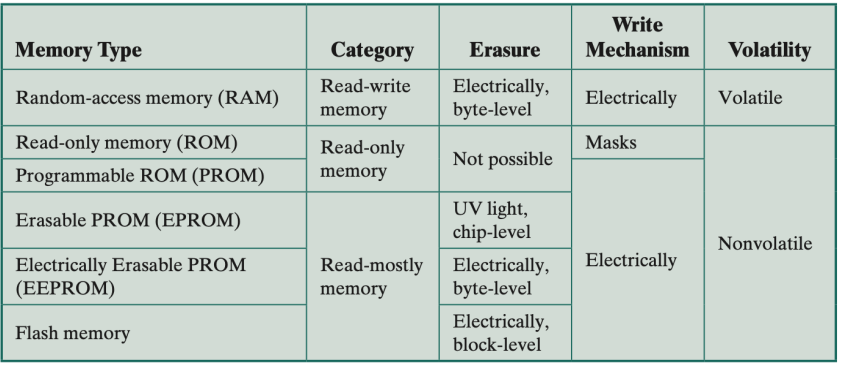
Semiconductor Memory Type

memory 的性能 (performance) 评估。access time，memory cycle time 与 transfer rate [见 Chapter 6 Memory Hierarchy pp.21-22]

传输时的 error detection & correction。对 a block of data 添加一位 parity bit (校验码)，标识数据中 \(1\) 的个数的奇偶性。correction 则需要更多 bits，如 Hamming code。


Cache Memory

其实并不是很绕的东西，看 PPT 硬是看了很久才搞清楚。笔记写了挺多，后来一看只觉杂乱无章。想了很久，发现通过伪代码描述 address mapping 是一个最佳的选择。

把 cache memory 与 main memory 想成两个数组 cache 与 memory，memory 的空间远远大于 cache，因此可以当作哈希表来用；但代价是访问 memory 的速度极慢。为了最小化 CPU 访问数据的平均速度，把访问次数较多的数据存入 cache；具体存入 cache 的什么位置？这个问题就是 address mapping 所要解决的。

cache 或 memory 储存的都是 data block，每个 block 中有 \(b\)​ 个 bytes (若 word-addressed 就是 words)。

single-level cache 的 principle 与 multi-level cache 是一致的。

Fully associative. 灵活，多对一，但效率低下。

1
2
3
4
5
6
7
8
9
10
11
def read(addr, cache):
    # BLOCK_SIZE: the number of bytes within a block
    # tag: aka block number
    tag, offset = addr // BLOCK_SIZE, addr % BLOCK_SIZE
    for cache_line in cache:
        if cache_line.tag == tag:
            return cache_line.data[offset]  # search hit
    data = memory[tag]
    # write data in cache with some append/replace policy
    write(data, cache, some_append_policy)
    return data[offset]

Direct-Map Organization aka 1-way Set Associative.

  • 若 cache 大小为 \(m\)，memory[0], memory[m], memory[2m]... 均对应 cache[0]
  • 大大提升了读取速度，但如果 CPU 同时需要 memory[0] 与 memory[m]，一对一就成了诅咒。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def read(addr, cache):
    block_number, offset = addr // BLOCK_SIZE, addr % BLOCK_SIZE
    # CACHE_SIZE: the number of cache lines in the cache, one block per line
    tag, line_number = block_number // CACHE_SIZE, block_number % CACHE_SIZE
    if line_number in cache:    # memory[line_number] not empty
        cache_line = cache[line_number]
        if cache_line.tag == tag:
            return cache_line.data[offset]
        else:
            data = memory[block_number]
            write(data, tag, line_number, cache)  
            return data[offset]
    else:
        data = memory[block_number]
        write(data, tag, line_number, cache) 
        return data[offset]

def write(data, tag, line_number, cache):
    cache[line_number].tag, cache[line_number].data = tag, data

K-way Set Associative. 引入 cache sets 综合了前两种地址映射机制。体现了读取效率和灵活性的 tradeoff。核心关系 \(m=k\times v\)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def read(addr, cache):
    block_number, offset = addr // BLOCK_SIZE, addr % BLOCK_SIZE
    # K-way: the number of cache lines in a cache set
    # SET_SIZE: the number of sets, SET_SIZE = CACHE_SIZE / K
    tag, set_number = block // SET_SIZE, block_number % SET_SIZE
    if set_number in cache:
        cache_set = cache[set_number]
        for cache_line in cache_set:
            if cache_line.tag == tag:
                return cache_line.data[offset]
        data = memory[block_number]
        write(data, tag, set_number, cache, some_append_policy)
        return data[offset]
    else:
        data = memory[block_number]
        write(data, tag, set_number, cache, some_append_policy)
        return data[offset]

常用的 replacement policy (direct map organization 的 set size 为 \(1\)，不需要 replacement policy)：FIFO (first-in-first-out)，LRU (least recently used) 与 RR (random replacement)。

两种 write policy。

  • write through - cache 与 main memory 的写入是 consistent 的。问题：main memory 的写入较慢 (但指令的执行并不会被其阻塞)，如果在写入完成之前，下一个指令要求访问该 memory slot，就会产生冲突。
  • write back - 仅仅在 cache 中的某个 memory block 被替换时更新 main memory。写入效率显著高于 write through。当存在 I/O operations 时，cache 与 main memory 的 inconsistency 会引发冲突。

从 direct-map organization，到 k-way associative，再到 fully associative，hit ratio (\(1-\)miss ratio) 越来越高，读写速率越来越慢。重要公式 \(\text{average access time }=\text{ hit time }+\text{ miss ratio }\times\text{ miss penalty }\)​

  • hit time: 在该 cache layer，一次 search hit 所需的时间。
  • miss ratio: search miss 发生的概率。
  • miss penalty: 若该 cache layer 是 L1，miss penalty 是 L2 的 average access time。若该 cache layer 是 L3，miss penalty 是 main memory 的 average access time。[见 Chapter 7.2 p.8 multi-level caches]


External Storage

这一节主要讲外部存储器。

首先是一些名词。

  • Magnetic disks (磁盘)。储存数据。
    • Cylinder - Sector - Track 结构。
    • Sector: Gap - Sync - Address mark - Data - ECC (error correction code) 结构。
  • Disk access 评估的三个重要时间参数。Seek (读写头在 cylinder 间移动)，Rotational delay (指定的 sector 移动到读写头处)，Data transfer time [公式见 Chapter 8 External Storage pp.8]
  • HDD (Hard Disk Drive, 硬盘驱动器)。各种磁盘是 HDD 的媒介。

关于 RAID (Redundant Array of Independent/Inexpensive Disks, 独立磁盘冗余阵列)，是一种多个磁盘的组织形式。关键概念：Data striping 把连续的数据分成小段分散在多个磁盘中以促进并行读/写。

课上共介绍了 6 个 standard RAID levels [Chapter 8 External Storage pp.11-23]：

  • RAID 0：应用 striping。I/O 效率高 (并行读写)，无冗余。
  • RAID 1：多了一个镜像磁盘 (mirrored backup)。
  • RAID 2：采用 Hamming code 作为 ECC，冗余磁盘的数量是 \(\log\) 数据磁盘的数量。
  • RAID 3：使用额外的一个冗余磁盘储存其他所有数据磁盘的 parity bit。\(X_r=\oplus_{i}^n X_i\)。
  • RAID 4：采用 block-level striping，这意味着每次读取的数据总是在一个磁盘内。(RAID 0-3 通常采用的是 byte-level 或 bit-level striping，读取一个 block 需要访问所有磁盘)
  • RAID 5：采用 block-level striping，且 parity strips 分散在所有磁盘中 (RAID 3-4 的 parity strips 统一存储在一个额外的冗余磁盘中)。
  • RAID 6：使用两个 parity stripes，应对两个 HDD failures。

关于 SSD (Solid State Disks/Drives, 固态硬盘/驱动器)。与 HDD 相比，I/O 效率，访问速率都高，耗能少，耐久高。


Input and Output

关于 I/O。

学到这里越来越发现计组知识本身不难，关键在于找到其中的逻辑联系。可惜的是，课件中所展现出来的逻辑非常的 unorganized (我本来想说课件简直是答辩，但其实它对于知识的描述和总结是很详实的，还是有其可取之处)。

开场陈述：I/O Modules 可视作是外部设备 (External Devices, aka Peripherals) 的接口；CPU (aka processor) 通过和 I/O Modules 交互对外部设备进行操纵。

CPU - I/O Modules interactions (direct)。

  • CPU 通过读写 I/O Modules 中的两种 registers 来完成交互。
    • The Control and Status Register CSR - 存储了外部设备的状态信息 (读)，对外部设备的操作 (写)，可分散在同一个 register 的多个 bits 中。
    • The Data Register - 存储了其他数据，例如向外部设备的输入等 (读/写)。使用了 Data Buffering 机制的 Data Register 常被称为 Buffer Register BR。
  • I/O Modules 的种类。
    • Port-mapped I/O。I/O Modules 中的 registers (如 CSR, BR) 作为独立的 dedicated I/O ports 的一部分，CPU 需要通过特定的指令对它们进行访问。
    • Memory-mapped I/O。I/O Modules 中的 registers 是 memory map 的一部分，CPU 能通过普通的 memory read/write 指令直接访问。

CPU - External Devices interactions (indirect)；有三种交互方式。

Programmed I/O。特征是 CPU 在空循环中等待 External Device 完成 I/O operations。以 read operation 为例：

  • CPU 向 I/O Modules 中的 CSR 发送一个 read 命令。
  • CPU 从 CSR 中获取外部设备的状态。
  • OK ? 从 BR 中读取数据 : 返回第二步继续循环。

Interrupt-Driven I/O。减轻 Programmed I/O 的 CPU 资源浪费。[见 Chapter 9 Input and Output pp.16-20] 这里只讲几个值得注意的细节。

  • CPU 收到 interrupt signal 后并不立即悬置程序，而是在当前指令执行完毕后再转向 interrupt attention。这是为了减少需要保存的 register 数量。
  • 需要保存到栈中的 registers：
    • Processor Status Word PSW, aka flag register，即前一个 ALU 的 result。当下一个指令是 branch 时将会用到这个值。
    • Program Counter PC。
    • 所有在 interrupt routine 中被用到的 registers，在使用之前都将被 push 到栈中进行保存。
  • interrupt routine 的最后一个指令是 Return from Interrupt RETI，它将会恢复 PSW, PC 与所有备份在栈中的 registers (in a reverse order that they were saved)。

Direct Memory Access (DMA)。在 I/O Modules 中引入 Input-Output Processor (IOP)。它无需 CPU 的直接干预，能够直接访问 memory。需要解决的问题是 IOP 与 CPU 的冲突：例如，它们需要同时访问同一块 memory。

引入 Cycle Stealing (周期挪用) 机制。即 IOP 向 CPU 发送信号请求 CPU 将 memory bus 的占用解除；如果 CPU 接下来的 cycle 无需访问 memory，它将同意请求，IOP 则会取得 memory bus 的控制。IOP 每次请求通常只占用一个或几个 cycles。


Instruction Set & Addressing

一些指令我们已经很熟悉了，在 Instruction Execution Cycle 那一章节有过介绍。

机器指令 (machine instruction) 的操作码 (operation code, opcode) 被各式各样的 mnemonics 表记。不同的机器可能有不同的缩写策略，但这些指令都能够大致分为以下几类：

  • data transfer - e.g. MOV, LD, ST
  • arithmetic - e.g., ADD, SUB
  • logical - e.g., AND, OR, NOT
  • transfer of control - BR for branch, CALL, RET for procedure

这里稍微分辨一下 arithmetic 和 logical 两种指令的区别：算术指令把 operands 视作数字，而逻辑指令把 operands 视作 bit pattern - 也就是说，逻辑指令直接操纵二进制串。

何以见得呢？考虑逻辑左/右移指令 (logical shift) 与算数左/右移指令 (arithmetic shift) 的区别。逻辑 shift 指令直接移动对应的 bit pattern，左移在 LSB 补零，右移在 MSB 补零。而算数 shift 指令会专门复制 sign bit 上的值不移动；这是因为算数 shift 指令本质上是对其所代表的数字进行乘 2 或除 2。

指令集架构 (instruction set architecture)。精简指令集运算 (Reduced Instruction Set Computing, RISC) - MIPS, ARM；复杂指令集运算 (Complex Instruction Set Computing, CISC) - x86, x86-64。

寻址模式 (addressing modes) 是指令集架构的重要组成部分，抽象了指令的寻址过程 (tradeoff 是更复杂的硬件实现)。这里的寻址对象当然是 memory 里的地址；现代处理器提供了大量 registers，大大降低了寻址需求。因此，常用的寻址模式被削减到了几种。

几个符号表记的规定：

  • A = contents of an address field in the instruction.
  • R = contents of an address field in the instruction that refers to a register.
  • EA = actual (effective) address of the location containing the referenced operand.
  • (X) = contents of memory location X.

Immediate Addressing (立即寻址) - 即命令直接提供 operand 的真实值。又称 literal mode。

1
2
3
# Value = A
MOV #200, R6
ADD R2, #4, R2

Direct/Absolute Addressing (直接寻址) - 命令提供 operand 的地址，而非值。

1
2
# EA = A
MOV A, R1 # Move the content at A to R1

Indirect Addressing (间接寻址) - 就是指针啦！命令提供一个地址，该地址中的值指向 operand 的地址。

1
2
# EA = (A)
MOV (A), R1 # Move the content pointed by the value at address A to R1. R1 = mem[A]

Register Addressing (寄存器寻址) - operand 的值储存在 general registers 中 (8 到 32 个)。register 的超快访问使其成为了现代处理器中使用得最多的寻址模式。

1
2
# EA = R
MOV R1, R2 # move the content of R1 to R2

Register Indirect Addressing (寄存器间接寻址) - 就是把 register 存储的值作为指针指向 operand 的地址。

1
2
# EA = (R)
MOV (R1), R2 # Move the content of mem[R1] to R2

Displacement Addressing (位移寻址) - operand 的地址被 register + 某个 offset 表示。

1
2
3
# EA = A + (R)
MOV A(R1), R2 # move the content at address A+R1 to R2. R2 = A[R1]
ADD R1, #4, R1 # R1 points to next word

Stack Addressing (栈寻址) - 部分机器提供 PUSH 与 POP 命令，用来访问栈。特殊的栈指针 (stack pointer) SP。

1
2
3
4
5
6
7
# EA = top of stack
PUSH R4:
    SUB SP, #4, SP
    MOV R4, (SP)
POP R3:
    MOV (SP), R3
    ADD SP, #4, SP


Assembly Language

在讲到这一节之前我们已经有一些汇编语言编程的基础了，这里稍微做一点补完。汇编语言的一条命令遵循以下形式：[label]: mnemonic [operand list] # comment。其中 mnemonic 表记又分以下两种：

  • 我们熟悉的 instruction，mnenomic 表示的是 operation codes。
  • assembler directives (有时也称作假指令 pseudo-instruction)，可以简单理解为汇编语言中一些方便的宏。常用的有 .data, .text, .globl [name], .word value1 [,value2],

举个例子：用汇编翻译最简单的 if-else 流程控制 x = a[0] > a[1] ? a[0] : a[1]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
    .data       # begin data segment
a:  .word 1     # create storage containing a[0] = 1
    .word 2     # create storage containing a[1] = 2
x:  .word 0     # create storage containing 4, x = 4
    .text       # begin program segment
main:
    LD #a, R0	# a is an array, use #a to indicate the address
    LD 0(R0), R1 
    LD 4(R0), R2 # notice 4!
    BGT R1, R2, else
    ST R2, x
    BR return
else:
    ST R1, x
return: 
    RET

此外，还有用汇编写函数 (function, aka procedure)。需要注意的是在函数开始时 PUSH 储存，结束时 POP 恢复。使用 CALL 调用函数。下面这个函数 Capitalize 把储存在 R0 中的小写字母改大写。

1
2
3
4
5
6
7
8
9
10
11
12
Capitalize:
    PUSH R1
    PUSH R2
    LD #0x61, R1  # 'a'
    LD #0x7a, R2  # 'z'
    BLT R0, R1, Ret
    BGT R0, R2, Ret
    SUB R0, #0x20, R0 # 0x20='a'-'A'
Ret:
    POP R1
    POP R2
    RET


Operating System

OS 是 software！它有以下功能：

  • program creation. 指 OS 能够调用一些 utility programs e.g. editor (vi, emacs), compiler (gcc), debugger (gdb), etc.
  • program execution. OS 把程序从 hard disk 加载到 main memory，准备执行程序所需的资源。
  • I/O access. OS 为程序提供一个统一的 I/O 接口。
  • file system management.
  • system access. OS 的 protection scheme: 某些特定的资源或动作只能在 kernel (supervisor) mode 下执行，user mode 没有直接访问的权限，通常通过 system call 来调用这些被保护的资源。
  • error detection and response.
  • accounting statistics.
  • multitasking and time-sharing. 我们知道 CPU 可以被多个进程共享，每个进程轮流占据一段 time slice。OS 将会处理 process scheduling。

虚拟内存 (Virtual Memory) 技术。

  • 使用 Hard Disk 扩充物理内存 (Physical Memory)。
  • 重定义地址空间，为程序提供连续的虚拟内存地址 (Virtual/Logical Address)。这在不浪费物理内存的同时，简化了大型程序的编写。虚拟地址到物理地址的映射是由内存管理单元 (Memory Management Unit, MMU) 完成的。

虚拟地址与物理地址均采用分页 (Paging)，将地址空间划分为若干页。维护地址映射关系的数据结构被称为分页表 (Page Table)，分页表由若干行 PTE (Page Table Entry) 组成，第 \(i\) 行记录的是第 \(i\)​ 页的信息。

  • V valid bit. 该页在内存中吗？若在，提供 physical frame number (PFN)。可以简单理解为物理地址分页的索引，对应的是虚拟地址中的 virtual/logical page number (VPN, LPN)，即当前的行数。
  • P protection info. 该页的 protection mode，如访问权限等 (r/w, supervisor/user access)。
  • D dirty bit 标记。若某页在 load 进 physical memory 之后被修改过，我们将其标记为 dirty；这意味着我们要将修改后的内容 write back 回 hard disk。

OK，那我们开始 address translation 吧！某个程序通过 CPU address bus 访问某个地址 addr：

  • 提取 VPN (LPN) 与 offset。addr=[VPN+offset]。
  • 找到对应的 VPN 对应的 PTE，查看 valid bit，检查该 page 是否在 physical memory 中。
  • 如果是，从 PTE 中 找到 PFN 并翻译成 physical address [PFN+offset]，并访问 physical memory。
  • 如果否，生成一个 page fault。

缺页异常 (page fault) 发生后，OS 将接管并 fetch required page from hard disk to memory。具体来说：

  • 从 hard disk 中获取对应的页。
  • 从 physical memory 中找到一个空白页。如果没有，replace (FIFO/LRU)。
  • 如果被 replace 的页是 dirty 的，将其 write back 回 hard disk，并修改对应 PTE 的 valid bit。
  • 把之前获取的页写入，并修改对应的 PTE。

Page Table 也有比较强的 locality 特征，因此也能套一层 cache - Translation Lookaside Buffer (TLB)。若 PTE 不在 TLB 中，先使用 Page Table，再把对应的 PTE cache 进 TLB。

等等，这个过程是不是太像 cache memory 了？还真是！看看这个 analogue：

Cache Virtual Memory
Block Page
Block Size Page Size
Block Offset Page Offset
Cache Miss Page Fault
Cache Tag Virtual Page Number (VPN)


Processor Organization

关于 control signal - data movement is controlled by control signals。

把一条指令拆成若干 data movements 的过程，我们可以将其分为以下几个阶段 (stages)：

  • Fetch Instruction (FI)
  • Decode Instruction (DI)
  • Calculate Addresses (CO) * 现代处理器是 register-to-register 的，往往没有 CO 阶段。
  • Fetch Operands (FO)
  • Execute Instruction (EI)
  • Write Operand (WO)

这直接促使了管道 (pipeline) 的产生。以上各个 stages 的 data movement 都是不相交的，因此它们可以被并行处理。在理想情况下，一个 5-stage pipeline 可以做到执行 one instruction per clock cycle，即 \(CPI = 1\)。

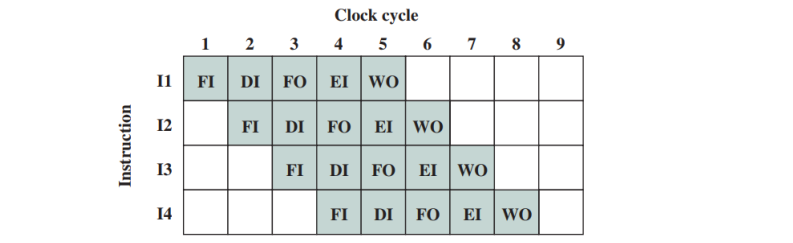
Five-stage pipeline, ideal case

然而，现实没这么理想。不同指令的 stage 不同，stage 所需的时间不同；指令间也可能存在先后顺序等依赖关系。我们把这种非理想的情况称为 Pipeline Hazards，即需要阻止下一条指令进入 pipeline 的情况。

Resource Hazard (Structural Hazard). 两条指令抢夺同一个 resource 的情况 (ALU, memory read port, etc.)。解决方法：添加更多 resources。

Data Hazard. e.g. \(I_1\) ADD R1 R2 R3，\(I_2\) SUB R3 R4 R4。这种情况下 \(I_2\) 必须等待 \(I_1\) 执行完毕。解决方法：调整程序逻辑，或 data forwarding (硬件方案)。三种 data hazards (仅有 RAW 发生在 pipeline 中):

  • Read after Write (RAW) hazard - \(I_1\) 写入 \(R\)，\(I_2\) 读取 \(R\)。读取发生在写入之前，hazard。
  • Write after Read (WAR) hazard - \(I_1\) 读取 \(R\)，\(I_2\) 写入 \(R\)。写入发生在读取之前，hazard。
  • Write after Write (WAW) hazard - \(I_1\) 写入 \(R\)，\(I_2\) 写入 \(R\)。\(I_2\) 的写入发生在 \(I_1\) 之前，hazard。

Control Hazard. 若 \(I_1\) 是一个 branch 指令，下一条指令必须等待 \(I_1\) 完成后才能开始 FI 阶段。缓解方法：Branch Prediction。下一条指令是跳转后的，还是无需跳转的？提前预测一个并作为 \(I_2\)。

Processor Performance 的几个指标。

  • Clock per Instruction (CPI).
  • Clock Rate: the number of cycles a processor can execute per second. 3GHz processor \(\to\)​ 3 billions cycles per second.
  • Execution Time (of a Program): \(\text{Instruction Count}\times CPI\times \text{Clock Cycle Time }\).

以 RISC (Reduced Instruction Set Computing) 为代表，现代处理器有哪些特点呢？

  • 除 LD, ST 需要涉及 memory access 外，所有指令均是 register-register 类型的。
  • Simple, Fixed-Length, and Fixed-Format instructions. (instruction count ++, but acceptable)
  • 精简的 operations 与 addressing modes。当需要考虑的情况较少时，CPU 与 pipeline 的设计也变得更加优雅高效。(clock rate ++)
  • Use of hardwired rather than microprogrammed control.
  • Extensive Pipelining: 使用各种 software 或 hardware techniques 尽可能地消除 pipeline hazards。(CPI --)
  • Use of Large Register File. CPU 的精简使得更多 registers 的使用成为可能。


Reference

  This article is a self-administered course note.

  References in the article are from corresponding course materials if not specified.

Course info: COMP2120, Prof. Zhao Qi

Course textbook: William Stallings, Computer Organization and Architecture (10th edition)

-----------------------------------そして、次の曲が始まるのです。-----------------------------------