归约的概念

The Idea of Reduction.

Reduction (or simulation) is a powerful idea in computer science. Especially in cryptography, we use the idea of reduction to prove security of some cryptographic primitives.

We will illustrate the idea of reduction with a concrete example.

Example: Pseudo One-time Pad

Try to prove: Pseudo OTP $\Pi$ is EAV-secure if $G$ is a PRG.

We reduce "Pseudo OTP $\Pi$ is EAV-secure" to "$G$ is a PRG".

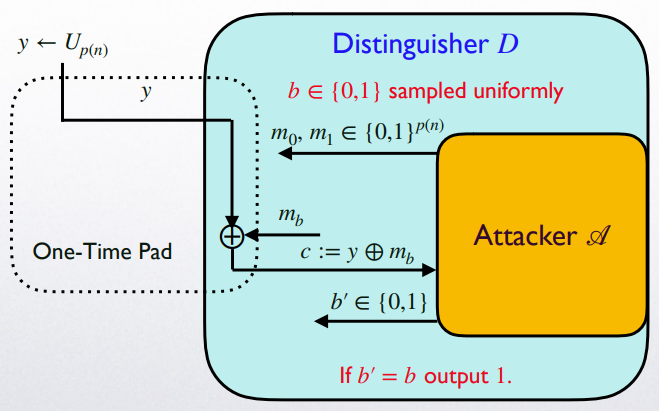
Construct a distinguisher $D$ for $G$ given $\mathscr{A}$ attacking $\Pi$ as its subroutine.

• $D$ runs $\mathscr{A}(1^n)$.
• $\mathscr{A}$ outputs $m_0,m_1$.
• $D$ generates a random bit $b\in\{0,1\}$ and obtain $r$ from PRG challenger.
• $D$ sends $m_b\oplus r$ back to $\mathscr{A}$.
• $\mathscr{A}$ finally outputs $b'$.
• If $b'=b$, $D$ outputs $1$, otherwise $0$.

Considering the following 2 cases:

• $r\leftarrow U_{n}$ is truly random

  In this case, the view of $\mathscr{A}$ is distributed identically to that of a true OTP protocol $\widetilde{\Pi}$ which obeys perfect secrecy, therefore $\Pr_{r\leftarrow U_{n}}[D(r)=1]=\Pr[b=b']=\Pr[\mathtt{PrivK}^{eav}_{\mathscr{A}, \widetilde{\Pi}}(n)=1]=\frac{1}{2}$.

• $r:=G(s)$ for some $s$ ($r$ is pseudorandom)

  In this case, the view of $\mathscr{A}$ when run as a subroutine of $D$ is that of the adversarial indistinguishability experiment of the Pseudo OTP $\Pi$, therefore $\Pr_{s\leftarrow U_m}[D(G(s))=1]=\Pr[b=b']=\Pr[\mathtt{PrivK}^{eav}_{\mathscr{A}, \Pi}(n)=1]$.

Reduction process:

Since $G$ is PRG: $|\Pr_{r\leftarrow U_{n}}[D(r)=1]-\Pr_{s\leftarrow U_m}[D(G(s))=1]|\leq \varepsilon(n)$.

From the 2 equality above: $|\Pr[\mathtt{PrivK}^{eav}_{\mathscr{A}, \Pi}(n)=1]-\Pr[\mathtt{PrivK}^{eav}_{\mathscr{A}, \widetilde{\Pi}}(n)=1]|\leq \varepsilon(n)$.

Therefore $\Pr[\mathtt{PrivK}^{eav}_{\mathscr{A}, \Pi}(n)=1]\leq \varepsilon(n)+\frac{1}{2}$, which indicates that pseudo OTP is EAV-secure.

Reduction Logic

Understand the abstraction is the key to understand reduction.

If we want to reduce the security of $\Pi'$ to the security of $\Pi$, we need to construct an adversary $\mathscr{S}$ for $\Pi$ given the adversary $\mathscr{A}$ for $\Pi'$ as its subroutine, which is to say, $\mathscr{S}$ employs (runs) $\mathscr{A}$ as a black box abstraction function (Encapsulation).

The reduction involves 4 logic statements:

• $p:$ $\exists\ \mathscr{S}$ that is able to attack $\Pi$ with non-negligible advantage.
• $q:$ $\exists \ \mathscr{A}$ that is able to attack $\Pi'$ with non-negligible advantage.
• $\lnot p:$ $\Pi$ is secure, which means $\mathscr{S}$ that could successfully attack $\Pi$ is NOT exist.
• $\lnot q:$ $\Pi'$ is secure, which means $\mathscr{A}$ that could successfully attack $\Pi'$ is NOT exist.

If $\mathscr{S}$ is constructed successfully, it will be able to attack $\Pi$ with non-negligible advantage. Therefore we could conclude that if $\mathscr{A}$ could attack $\Pi'$ successfully, $\mathscr{S}$ (which takes $\mathscr{A}$ as its subroutine) could attack $\Pi$. The corresponding logic is $q\to p$.

According to the contrapositive statement, we have $\lnot p\to \lnot q$, which implys that the security of $\Pi$ guarantees the security of $\Pi'$. Therefore, the reduction is completed: we reduce the security of $\Pi'$ to the security of $\Pi$.